Com o objetivo de melhorar a segurança de seus territórios, o rei da Nlogônia decidiu contratar vigilantes. O pagamento do serviço é em barras de ouro, e o cálculo da quantidade necessária é um tanto peculiar.

Um território é composto por um conjunto de povoados que são representados por um identificador único inteiro. Se existe um caminho de $u$ para $v$, então o mesmo caminho é válido de $v$ para $u$, e ambos estão no mesmo território. O custo para a melhoria da segurança de um único território é calculado a partir da operação $OR$ entre todos os identificadores únicos dos povoados que compõem esse território.

Como o reino possui inúmeras terras e os valores podem ser bastante elevados, o rei propôs uma aposta para a empresa que gerencia os seguranças, de modo que o preço pode aumentar substancialmente ou diminuir consideravelmente: depois de calcular o valor para cada território, é aplicada a operação $XOR$ entre todos esses valores, sendo este o novo preço a ser cobrado.

A sua tarefa é calcular o novo preço.

Entrada

A entrada é composta por um único caso de teste.

A primeira linha possui dois números inteiros $N$ e $M$ ($1 \leq N \leq 2 * 10^5$, $0 \leq M \leq min((N * (N - 1) / 2), 2 * 10^6)$), representando o número de povoados (com identificadores de $1$ a $N$) e o número de conexões entre os povoados, respectivamente.

As próximas $M$ linhas possuem dois números inteiros $u_i$ e $v_i$, representando a conexão entre os dois povoados $u_i$ e $v_i$.

Saída

A saída é composta por um único valor inteiro: o preço total do serviço.

Dica: Na linguagem C, os operadores binários (considere a e b números arbitrários):
$OR$: a|b
$XOR$: a^b

Exemplos

Exemplo de entrada

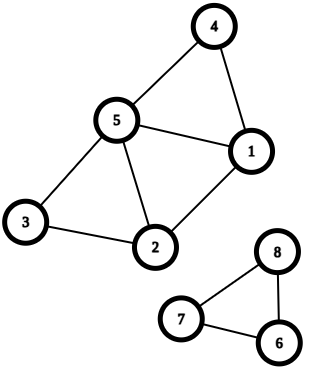
8 10
1 2
2 3
4 5
1 4
5 3
5 2
5 1
6 7
7 8
8 6

Saída para o exemplo acima

8

Explicação: Temos dois territórios distintos: {{$1, 2, 3, 4, 5$}, {$6, 7, 8$}}. Primeiro, é calculado o preço resultante para cada território aplicando a operação $OR$, resultando em $7$ e $15$. Para o preço final, aplicamos a operação $XOR$ entre os valores obtidos. Logo, a resposta é $8$.

Exemplo de entrada

3 0

Saída para o exemplo acima

0

Note que um povoado isolado é considerado um território.

Exemplo de entrada

10 7
1 2
2 3
3 4
5 6
6 7
7 8
9 10

Saída para o exemplo acim

3