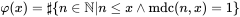
Neste exercício, você colocará em prática alguns conhecimentos de aritmética de inteiros através de uma função interessante cujo nome faz referência ao matemático suíço Leonhard Euler, quem a determinou.
A função totiente, por vezes referida por função tociente ou função (fi) é defenida para um número natural x como sendo igual a quantidade de números menores ou igual a x co-primos com respeito a ele.
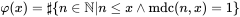
Por exemplo, , uma vez que 1, 3, 5 e 7 são co-primos de 8.
A função totiente é importante porque fornece o tamanho do grupo multiplicativo de inteiros módulo n – mais precisamente, é a cardinalidade do grupo de unidades do anel Z/nZ.
Para este problema, você deverá implementar um programa que leia um número natural menor que 65536 e calcule a função totiente de Euler para .
A entrada é composta por um número natural maior do que 1 e menor que 65536.
Caso não pertença ao conjunto dos naturais, a mensagem ‘entrada invalida.’ deverá ser apresentada.
Caso seja o número natural 1, a mensagem ‘entrada invalida.’ deverá ser apresentada.
Caso pertença ao conjunto dos naturais maiores do que 1, a resposta deverá ser o valor da função totiente de Euler para .
-1entrada invalida.1entrada invalida.5465535327686453431440